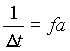 [3.1]
[3.1]In diesem Kapitel werden die systemtheoretischen Grundlagen erläutert, die im Projekt zur praktischen Anwendung kommen.
3.1 Zeitdiskrete Signalverarbeitung und Faltungsoperation
Ein Zeitkontinuierliches Signal (Abb. 3.1a) liegt nach einer Digitalisierung als zeitdiskrete Wertefolge vor (Abb. 3.1b), da bei der Digitalisierung eine Abtastung des Signals in definierten Zeitabständen D t erfolgt, wobei sich aus:
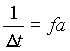 [3.1]
[3.1]
die Abtastfrequenz fa ergibt.
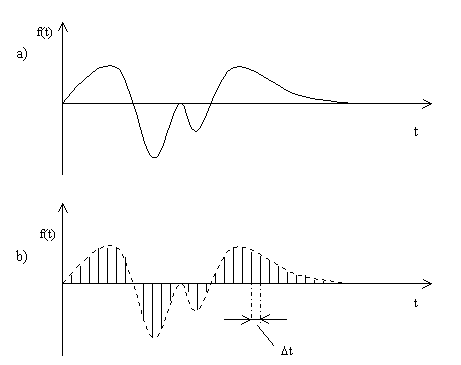
Abb. 3.1: Zeitkontinuierliche und zeitdiskrete Wertefolge
Es wird deutlich, daß die Abtastfrequenz ausreichend hoch sein muß, um den Signalverlauf möglichst genau digitalisieren zu können. Das Verhältnis von Abtastfrequenz zur maximal fehlerfrei digitalisierbaren Signalfrequenz ist durch das Shannon-Theorem3 gegeben, welches besagt, daß die Abtastfrequenz mindestens doppelt so hoch sein muß, wie die höchste abzutastende Signalfrequenz.
Nyquist beschrieb diesen Sachverhalt in ähnlicher Form, so daß in dem Zusammenhang auch oft vom Nyquist-Theorem oder Nyquist-Kriterium4 gesprochen wird.
Bei gegebener Abtastfrequenz – in der beschriebenen Schaltung liegt sie bei 48 kHz – muß das Eingangssignal somit durch Tiefpaßfilterung auf maximal 24 kHz begrenzt werden. Bei den Analogeingängen bewerkstelligt dies das im AD-Wandler implementierte Tiefpaßfilter (=Aliasingfilter), den Digitaleingängen wird das Signal bereits gefiltert zugeführt.
Nimmt man aus der zeitdiskreten Wertefolge einen Abtastwert heraus, so erhält man einen Nadelimpuls mit definierter Höhe und Breite (D t). Er kann aber annähernd als Dirac- oder Deltaimpuls betrachtet werden, der eine Breite von 0 bei unendlicher Höhe besitzt5. In der Praxis reicht diese Annäherung in den meisten Fällen aus.
Ein zeitdiskretes Signal kann somit als eine Folge gewichteter Diracimpulse betrachtet werden.
Wird ein einzelner Nadelimpuls in ein zu analysierendes, lineares System geführt, so erhält man eine vom Systemverhalten abhängige Impulsantwort (Abb. 3.2):
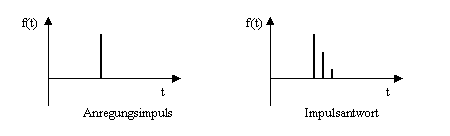
Abb. 3.2: Impulsantwort eines linearen Systems (Beispiel)
Von einem linearen System wird gesprochen, wenn die mit den Koeffizienten gewichtete Summe der Eingangswerte eine Folge erzeugt, die der ebenso gewichteten Summe der Ausgangsfolge des Systems entspricht (Superpositionsprinzip), wobei die Koeffizienten das Systemverhalten bestimmen6. Ein lineares System ist die Voraussetzung für die in diesem Kapitel aufgeführten Grundlagen.
Besteht das Anregungssignal nicht aus einem Einzelimpuls sondern aus einer Impulsfolge, so kann bei entsprechender Auslegung dieser Eingangsimpulsfolge das nicht ideale Systemverhalten kompensiert werden (Abb. 3.3):
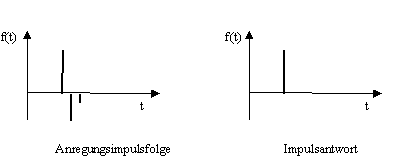
Abb. 3.3: Impulsantwort eines linearen Systems bei kompensierendem Eingangsignal
In der Praxis besteht das dem System zugeführte Signal jedoch nicht aus einem Einzelimpuls sondern aus einer Eingangsimpulsfolge (Audiosignal). Wie bereits oben aufgeführt, kann eine Impulsfolge aber als eine Folge gewichteter Einzelimpulse betrachtet werden.
Somit gilt folgende Schlußfolgerung:
Das Ausgangssignal läßt sich aus der Überlagerung der Impulsantwort eines Systems mit den Einzelwerten der Eingangsimpulsfolge bestimmen.
(Anm.: Diese Schlußfolgerung geht auch aus der oben aufgeführten Beschreibung eines linearen Systems hervor).
Wird jeder Einzelimpuls der Eingangsimpulsfolge mit der kompensierend wirkenden Anregungsimpulsfolge gewichtet und summiert, so ergibt sich eine Korrekturimpulsfolge, die dem System zugeführt wird und das nicht ideale Verhalten des Systems aufhebt.
Die Anregungsimpulsfolge besteht aus mehreren Einzelimpulsen, die als Koeffizienten bezeichnet werden.
Mathematisch ergibt sich somit folgender Sachverhalt (Beispiel für zwei Koeffizienten):
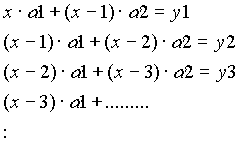
x = aktueller Wert x-1 = vorangegangener Wert
a 1 = 1. Koeffizient a 2 = 2. Koeffizient
Als Summe ausgedrückt ergibt sich folgende Gleichung:
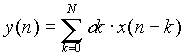 [3.2]
[3.2]
Diese Formel entspricht der mathematischen Operation einer diskreten Faltung7, die im übrigen auch für ein FIR-Filter gilt8.
Ein FIR-Filter führt somit eine Faltungsoperation aus.
Aus Gleichung [3.2] und aus der zuvor beschriebenen Herleitung ergeben sich folgende Eigenschaften eines FIR- Filters9:
Im vorliegenden Projekt kommt ein FIR-Filter zum Einsatz. Die Audiodatenfolge wird mit einer Koeffizientenfolge gefaltet, das Ergebnis in analoge Signale gewandelt und über einen Verstärker dem Lautsprecher kontinuierlich zugeführt. Der Lautsprecher samt der Übertragungsstrecke stellt das lineare, aber nicht ideale System dar.
Demnach muß zunächst eine Filterkoeffizientenfolge ermittelt werden, die das nicht ideale Systemverhalten kompensiert. Dies erfolgt unter Zuhilfenahme der Fouriertransformation.
3.2 Fourierreihen und Fouriertransformation
Die Fouriertransformation ermöglicht mit Hilfe der Impulsmeßtechnik die Ermittlung der für das FIR-Filter benötigten Koeffizienten. Zunächst werden hier die theoretischen Grundlagen der Fourierreihen sowie der Fouriertransformation erläutert.
Joseph de Fourier zeigte, daß jede beliebige periodische Zeitfunktion in diskrete harmonische Schwingungen einer Grundfrequenz und deren ganzzahlige Vielfache zerlegen werden kann, wobei die Grundfrequenz dem Kehrwert der Periodendauer entspricht.
Dies läßt sich mathematisch als sog. Fourierreihe ausdrücken10 11 12 :
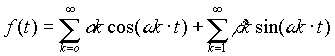 [3.3]
[3.3]
wobei a k und b k die Fourierkoeffizienten darstellen, die die Amplituden und Phasenlagen der einzelnen Schwingungen ergeben.
Somit wird eine Funktion, hier eine Zeitfunktion, in einen anderen Existenzbereich, in diesem Falle den Spektralbereich, überführt, was als Transformation, in diesem Falle als Fouriertransformation bezeichnet wird.
Üblicherweise erfolgt die Schreibweise in komplexer Notation und mit verschobener Zeitachse, d.h. der Index k nimmt negative Werte an, was aber am Funktionsverlauf nichts ändert:
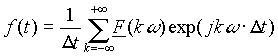 [3.4]
[3.4]
wobei ![]() mit fp =
Grundfrequenz
mit fp =
Grundfrequenz
und 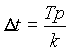 mit Tp =
Periodendauer
mit Tp =
Periodendauer
Die Fourierkoeffizienten a k und b k sind hier zur komplexen Koeffizientenfolge F(kw ) zusammengefaßt. Mit Hilfe der in Gleichung [3.5], [3.6], [3.7] dargestellten Rechenvorschriften lassen sich die Koeffizienten umrechnen und nach Betrag und Phase darstellen:
![]() [3.5]
[3.5]
![]() [3.6]
[3.6]
 [3.7]
[3.7]
Gleichung [3.4] läßt erkennen, daß sich nur an den Stellen ![]() (Spektral-)Werte
ergeben, was auch bereits aus der eingangs erwähnten Definition
der Fourierreihe hervorgeht.
(Spektral-)Werte
ergeben, was auch bereits aus der eingangs erwähnten Definition
der Fourierreihe hervorgeht.
Da die Zeitfunktion nur durch die Grundschwingungen und deren ganzzahlige Vielfache rekonstruiert wird, können auch nur Spektralwerte bei einem Vielfachen der Grundfrequenz existieren. Der Abstand der Spektralwerte ist somit gegeben durch (siehe auch Abb. 3.4):
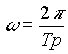 bzw.
bzw. 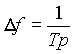 [3.8]
[3.8]
D.h., je länger die Periodendauer Tp ist, desto niedriger ist zum einen die darstellbare Grundfrequenz fp des Signals, und desto kleiner wird zum anderen der Abstand der Spektralwerte.
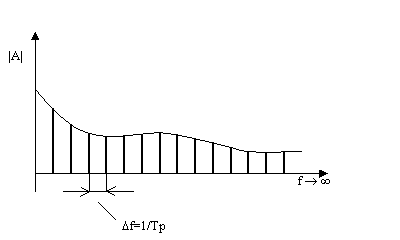
Abb. 3.4: Linienspektrum (Amplitude) bei periodischer Signalfunktion
Die Anzahl der errechneten Spektralwerte ist gegeben durch k und geht somit gegen unendlich; folglich strebt die obere Grenzfrequenz auch gegen unendlich, was allerdings nur mathematisch relevant ist.
In der Praxis muß man die Folge bei einer bestimmten Anzahl k = n abbrechen, um zu einem Ergebnis zu kommen:
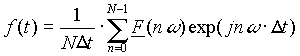 [3.9]
[3.9]
Da der Abstand der Spektralwerte gleich der Grundfrequenz ist (Gleichung [3.8]), ist die maximal darzustellende obere Grenzfrequenz gegeben durch:
![]() [3.10]
[3.10]
Es wurde gezeigt, daß die komplexen Koeffizienten F(nw ) bzw. deren Umrechnung in Betrag und Phase die gesuchten Spektralfunktionen ergeben. Somit sollte Gleichung [3.9] wie folgt umgestellt werden:
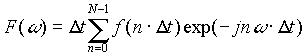 [3.11]
[3.11]
Die bisherige Betrachtungsweise bezog sich ausschließlich auf kontinuierliche Zeitfunktionen. Sie kann aber ohne weiteres auf abgetastete, diskrete Zeitfunktionen übertragen werden.
Hierbei wird D t zur Abtastrate Ta, woraus sich folgende Formel ergibt:
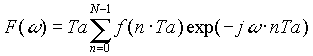 [3.12]
[3.12]
w ist auch hier nach wie vor die Kreisfrequenz der Grundperiode Tp und müßte somit im Prinzip mit einem Index versehen werden. In der Literatur wird w daher oftmals komplett durch den Buchstaben "m" ersetzt.
Bei der Fourierreihenentwicklung einer kontinuierlichen Zeitfunktion ist die Anzahl der Spektralwerte gegeben durch den Index "n" und somit unabhängig von der zu untersuchenden Periodenlänge frei wählbar. Bei abgetasteten Signalen ist jedoch die Anzahl "n" der Abtastwerte durch die konstante Abtastrate Ta festgelegt und somit von der Periodenlänge abhängig:
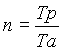 [3.13]
[3.13]
Der Abstand der Spektrallinien ist nach wie vor gegeben durch die Periodendauer Tp:
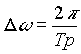 [3.14]
[3.14]
Die Anzahl der Spektrallinien legt über Gleichung [3.12] jedoch die höchste darzustellende Frequenz dar. Der Anwender hat also bei der Analyse von Abtastsignalen für ausreichend kleine Abtastraten, also hohe Abtastfrequenzen, zu sorgen, um die höchsten im Signal enthaltenen Frequenzen sicher erfassen zu können. Das o.g. Shannon-Theorem enthält die entsprechenden Vorgaben bereit.
Die bisherige Betrachtungsweise bezog sich ausschließlich auf periodische Signalverläufe der Periodendauer Tp. Eine Erweiterung der Sachverhalte auf in der Praxis wesentlich häufiger vorkommende nichtperiodische Signale ist bei der diskreten Signalanalyse nicht möglich, denn der Exponentialterm der Gleichung [3.12] ist mit 2p periodisch:
![]() [3.15]
[3.15]
wobei 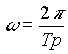
umgestellt ergibt sich:
![]()
wobei ![]()
Daraus folgt:
![]()
Somit ist das Spektrum mit 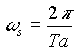 ebenfalls periodisch.
ebenfalls periodisch.
Da sich die Gleichung [3.12] nach f(t) umstellen läßt, kann ein Frequenzspektrum wieder in eine Zeitfunktion rücktransformiert werden.
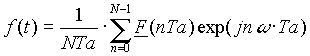 [3.16]
[3.16]
Im Exponentialterm hat sich, abgesehen vom Vorzeichen, nichts geändert. Demnach ist auch die rücktransformierte Zeitfunktion periodisch, und zwar mit:
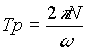 [3.17]
[3.17]
D.h. bei der Analyse eines Signalausschnitts muß immer Periodizität angenommen werden, denn spätestens durch die Rechenvorschriften ergibt sich ohnehin eine Periodizität, die erheblichen Einfluß auf das Transformationsergebnis haben kann, z.B. wenn sich an den Signalenden Sprungstellen befinden.
Des weiteren lassen sich zwar formal aus N Abtastwerten N Spektralwerte errechnen, aber ab der Hälfte der Abtastwerte
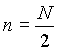
wiederholt sich das Spektrum. Somit erhält man bei einer
Fouriertransformation für N Abtastwerte nur ![]() relevante Spektralwerte.
relevante Spektralwerte.
Aus diesem Grund wird die Transformation häufig nicht über n
= 0 bis N-1, sondern über 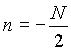 bis
bis 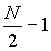 durchgeführt (Gleichung [3.18]), damit die relevanten Werte z.B.
in einer graphischen Darstellung beim Nullwert der X-Achse
beginnen (Abb. 3.5).
durchgeführt (Gleichung [3.18]), damit die relevanten Werte z.B.
in einer graphischen Darstellung beim Nullwert der X-Achse
beginnen (Abb. 3.5).
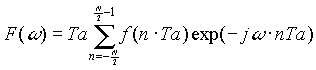 [3.18]
[3.18]
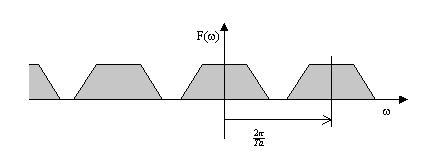
Abb. 3.5: Amplitudenspektrum eines bandbegrenzten Signals
Aus Abbildung 3.5 wird weiterhin deutlich, daß die Abtastfrequenz mindestens das Doppelte der im Signal enthaltenen höchsten Frequenz betragen sollte (Shannontheorem). Andernfalls würden sich die Spektren überschneiden.
Wie bereits gezeigt wurde, ist bei einer diskreten Signalanalyse die Anzahl der durch Ta und Tp gegebenen Spektrallinien begrenzt. Bei einer Rücktransformation in den Zeitbereich kann somit das Zeitsignal nur aus einer begrenzten Anzahl harmonischer Schwingungen gebildet werden. Dies führt gerade bei Sprungfunktionen (z.B. bei Rechtecksignalen, siehe Abb. 3.6), in deren Flanken hohe Frequenzen enthalten sind, zu Rekonstruktionsfehlern – es stehen nicht genügend harmonische Schwingungen niedriger Periodendauer zur Verfügung. Dieses Phänomen wird auch als GIBBsches Phänomen13 bezeichnet.

Abb. 3.6: GIBBsches Phänomen
Eine Erhöhung der oberen Grenzfrequenz beseitigt das Problem übrigens nicht; es beeinflußt lediglich die Periodendauer der Ein- und Ausschwingvorgänge, nicht deren Amplitude.
Besteht das Zeitsignal lediglich aus einem Diracimpuls, so zeigt die Fourieranalyse folgendes Ergebnis (Abb. 3.7):
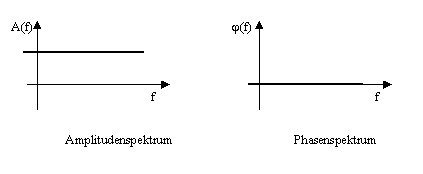
Abb. 3.7: Amplituden-und Phasenspektrum eines Diracimpulses
In einem Diracimpuls sind somit alle Frequenzen ohne Phasenverschiebungen enthalten. Diese Eigenschaften macht man sich in der Meßtechnik und auch im vorliegenden Projekt zunutze. Mit einem Diracimpuls regt man ein zu messendes System (in diesem Falle den Lautsprecher) in allen Frequenzbereichen an und kann durch die Fourieranalyse der Impulsantwort das Amplituden- und Phasenspektrum des Systems ermitteln. Der Ablauf wird im folgenden Beispiel noch einmal verdeutlicht (Abb. 3.8):
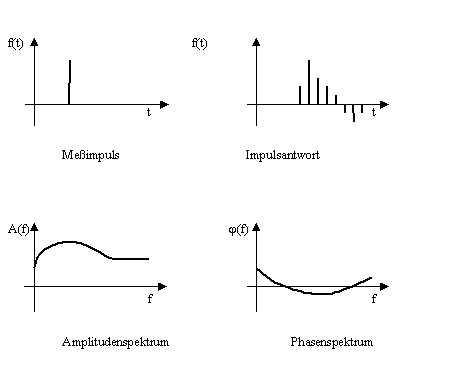
Abb. 3.8: Ermittlung des Amplituden- und Phasenspektrums eines Systems
Da die Fouriertransformation (Gleichung [3.12]) umkehrbar ist, kann aus einem beliebig vorgegebenen Amplituden- und Phasenspektrum durch Rücktransformation die Impulsantwort ermittelt werden. Invertiert man die Kurvenverläufe des Amplituden- und Phasenspektrums eines zuvor analysierten Systems und ermittelt hieraus durch Rücktransformation wiederum eine Zeitfunktion, so hat man eine Systemimpulsantwort kreiert, die gegenüber der eigentlichen, gemessenen Impulsantwort umgedrehtes Verhalten zeigt. Würde man die soeben durch die Invertierung der Kurvenverläufe ermittelte Impulsfolge dem System zuführen, könnte sie das Systemverhalten kompensieren. Die folgenden Diagramme verdeutlichen den Sachverhalt (Abb. 3.9):
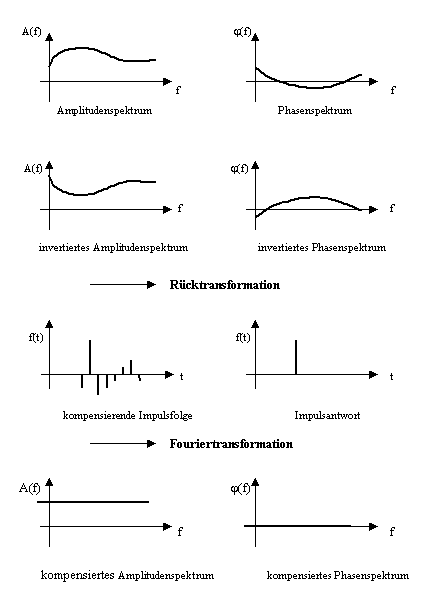
Abb. 3.9: Ablauf der Kompensierung eines nicht idealen Systemverhaltens
Statt eines Diracimpulses wird somit dem System die kompensierend wirkende Impulsantwort zugeführt, die das nicht ideale Verhalten des Systems aufhebt.
Diese kompensierend wirkende Impulsantwort ist jedoch die im vorherigen Kapitel 3.1 gesuchte Größe. Sie bildet die Filterkoeffizienten des FIR-Filters, welches nun diese Koeffizienten mit der dem System (Lautsprecher) zugeführten Eingangsimpulsfolge (digitalisiertes Musiksignal) faltet und somit die Amplituden- und Phasenfehler des Lautsprechers aufhebt.
Durch die Fourieranalsyse war es also möglich, die im Kapitel 3.1 gesuchten FIR-Filterkoeffizienten zu ermitteln.
Allerdings führt eine mit einem Diracimpuls durchgeführte Messung kaum zu brauchbaren Ergebnissen. Abhilfe schafft eine kurze Impulsfolge als Meßsignal. Deren Theorie wird im nächsten Abschnitt genauer beschrieben.
3.3 Impulsmeßtechnik
Bei der im Projekt verwendeten Samplingfrequenz von 48 kHz
beträgt die Länge einer Abtastperiode ![]() . Ein zur Lautsprechermessung
verwendeter, angenäherter Diracimpuls kann somit nur diese
minimale Impulsbreite erreichen.
. Ein zur Lautsprechermessung
verwendeter, angenäherter Diracimpuls kann somit nur diese
minimale Impulsbreite erreichen.
Selbst bei einer hohen Signalamplitude ist ein so kurzer Impuls im Lautsprecher kaum zu hören und bei der Mikrofonmessung verschwindet er fast im Grundrauschen. Eine Vergrößerung der Impulsbreite würde zwar den Energieinhalt und damit auch die Lautstärke erhöhen, aber der Meßimpuls wäre ein großes Stück weiter vom Ideal des (unendlich kurzen) Diracimpulses entfernt, was bei der anschließenden Transformation zu starken Abweichungen sowohl im Amplituden- als auch im Phasenspektrum führen würde.
Abhilfe schafft die Durchführung der Messung mittels einer kurzen Impulsfolge. Als Beispiel sei die Impulsfolge in Abb. 3.10 gegeben:
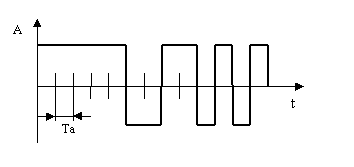
Abb. 3.10: Meßimpulsfolge (Barkerimpuls)
Die oben dargestellte Meßimpulsfolge ist weit vom Ideal des Diracimpulses entfernt, allerdings läßt er sich unter Zuhilfenahme der Korrelationsfunktionen trotzdem verwenden.
3.3.1 Autokorrelationsfunktion
Bei einer Autokorrelation werden die in einem Zeitsignal enthaltenen Abhängigkeiten untersucht. Wenn in einem Signal benachbarte Funktionswerte nicht mehr voneinander unabhängig sind, sind sie miteinander korreliert14.
Die Vorgehensweise ist dabei relativ einfach. Jeder Abtastwert wird der Reihe nach zunächst mit sich selbst multipliziert und zum letzten Wert aufaddiert. Im nächsten Schritt wird jeder Abtastwert mit seinem benachbarten Wert multipliziert und aufaddiert, anschließend werden die Abtastwerte im Abstand zwei miteinander verglichen, dann die im Abstand drei usw. . Das Ergebnis ist wiederum ein Zeitsignal und kann in folgende Gleichung [3.19] gefaßt werden:
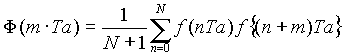 [3.19]
[3.19]
Beispiel:
Ein digitales Rauschsignal (Pseudo Random Noise) weist über eine gewisse Abtastperiode keinerlei Ähnlichkeiten innerhalb des Signals auf; es ist nicht korreliert. Somit ergibt die Autokorrelation einer Rauschfolge etwa folgenden Signalverlauf (Abb. 3.11):

Abb. 3.11: Autokorrelation einer Rauschfolge
Die Autokorrelation einer Rauschfolge (Abb. 3.11) besitzt in nur einem Punkt ein hohes Maximum, es ist somit nur an einer Stelle korreliert, und zwar dort, wo die Abtastwerte mit sich selbst verglichen werden. Die Höhe des Maximums und das Verhältnis zu den "Nebenzipfeln" hängt von der Länge der Rauschfolge ab. Ein Großteil der Energie der gesamten Rauschfolge enthält nach einer Korrelation das eine Maximum.
Dies wird in der Meßtechnik genutzt. Statt eines einzelnen Diracimpulses mit seinem zu geringen Energieinhalt wird ein Rauschsignal zur Messung verwendet und anschließend korreliert. Das Ergebnis ist quasi ein Diracimpuls (bzw. eine Diracimpulsantwort), der nun z.B. transformiert werden kann.
3.3.2 Kreuzkorrelationsfunktion
Die Kreuzkorrelation (Gleichung [3.20]) ist der Autokorrelation sehr ähnlich. Das Zeitsignal wird aber nicht mit sich selbst verglichen, sondern mit einer zweiten Signalfolge:
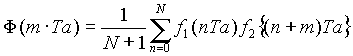 [3.20]
[3.20]
Die Kreuzkorrelation wird häufig in der Signalanalyse verwendet. Oft wird eine Systemantwort mit dem Anregungssignal kreuzkorreliert. Beeinflußt das System den Signalverlauf nicht, sind also Anregungs- uns Ausgangssignal identisch, wird das Signal mit sich selbst kreuzkorreliert, was einer Autokorrelation gleichkommt.
Die Korrelation des Barkerimpulses aus Abbildung 3.10 ergibt folgenden Signalverlauf.:
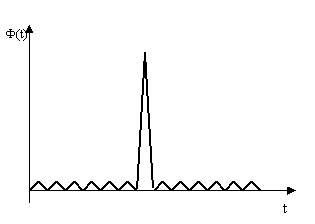
Abb. 3.12: Autokorrelation des Barkerimpulses
Trotz der geringen Länge erreicht der Barkerimpuls ein gutes Verhältnis von Maximum zu "Nebenzipfeln". Deshalb wurde dieser Impuls, er fand übrigens Verwendung in der Radartechnik15, im vorliegenden Projekt als Meßgröße benutzt. Die gemessene Impulsantwort wird mit dem Barkerimpuls kreuzkorreliert und weiterverarbeitet. Versuche mit kurzen Rauschsequenzen brachten nicht die gewünschten Erfolge und zur Aufzeichnung längerer Rauschfolgen reichte der Speicherplatz nicht aus.
3.4 Zusammenfassung und praktische Erwägungen
Die vorherigen Abschnitte haben gezeigt, daß die eigentliche Korrektur der Lautsprecher über ein FIR-Filter erfolgt, welches die hereinkommenden Audiosamples mit den Filterkoeffizienten faltet und somit bei richtiger Auslegung dieser Koeffizienten das Audiosignal in einer Weise beeinflußt, die zur Aufhebung der Frequenz- und Phasengangfehler der Lautsprecher führt. Zur Ermittlung der Filterkoeffizienten muß die Impulsantwort der Lautsprecher ermittelt werden. Um eine bessere Signalqualität zu gewährleisten, wird anstelle eines Einzelimpulses eine Barkerimpulsfolge für die Messung verwendet, deren Kreuzkorrelation mit der Lautsprecherimpulsantwort die geforderte Diracimpulsantwort ergibt.
Durch Fouriertransformation erhält man den Frequenz- und Phasengang der Lautsprecher. Die invertierten Verläufe dieser Frequenz- und Phasengänge werden rücktransformiert und ergeben die geforderten, fehlerkompensierenden FIR- Filterkoeffizienten.
Im Abschnitt 3.2 wurde gezeigt, daß die niedrigste noch erfassbare untere Frequenz fp von der Größe des Signalausschnitts (Periodendauer Tp) abhängt:
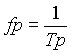 [3.21]
[3.21]
Ziel war es, eine Korrektur über den ganzen Hörbereich, also bis hinunter zu 20 Hz, vornehmen zu können. Somit muß die Meßperiodendauer mindestens 50 ms betragen. In dieser Meßspanne laufen etwa 2400 Abtastwerte auf; daraus folgt, daß ebenfalls 2400 Filterkoeffizienten ermittelt werden, demnach also ein FIR-Filter 2400ster Ordnung benötigt wird! Im vorliegenden Projekt wurde diese Zahl nicht ganz erreicht, sie beträgt 2048 und setzt somit die untere Grenzfrequenz auf 23 Hz herauf.
Der Abstand der Spektrallinien ist gegeben durch ihre Anzahl N der Abtastwerte innerhalb der Periodenlänge und der Samplingfrequenz:
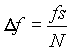 [3.22]
[3.22]
Allerdings ist zu berücksichtigen, das sich die
Spektrallinien bei ![]() wiederholen, so daß nur die Hälfte der Linien genutzt werden
kann. Darum endet der darstellbare Bereich bei der halben
Abtastfrequenz (Anm.: Dies ist wiederum eine Konsequenz des
Shannon-Theorems).
wiederholen, so daß nur die Hälfte der Linien genutzt werden
kann. Darum endet der darstellbare Bereich bei der halben
Abtastfrequenz (Anm.: Dies ist wiederum eine Konsequenz des
Shannon-Theorems).
Bei der Samplingfrequenz von 48 kHz und der auf 2048 reduzierten Anzahl der Abtastwerte beträgt die Frequenzauflösung somit etwa 23,5 Hz.
Mag diese Auflösung im Hochtonbereich noch genügen, so führt sie im Baßbereich zu Problemen, denn eine Beeinflussung des Frequenz- und Phasengangs ist nur über diese diskreten Spektrallinien möglich. Hier wäre eine bessere Frequenzauflösung wünschenswert, was allerdings nur über eine Vergrößerung der Meßperiodendauer und dementsprechend mehr Abtastwerten möglich wäre. Allerdings würde sich die Anzahl der Filterkoeffizienten in demselben Maße erhöhen, was das FIR-Filter vor unlösbare Aufgaben stellt.
Allerdings kann die Auflösung künstlich erhöht werden, indem die vorhandene Meßreihe am Ende mit Nullen aufgefüllt wird ("zero-padding"). Die Nullen haben keinen Einfluß auf das Meßergebnis, erhöhen aber die Anzahl der Abtastwerte und somit die Frequenzauflösung. Die untere Grenzfrequenz sinkt dadurch allerdings nicht, da sie durch die vorangegangene, mit kürzerer Periodendauer vorgenommene, Messung bereits festgelegt wurde. Im Projekt wird durch zero-padding die Anzahl der Meßwerte auf 8192 erhöht, was eine Frequenzauflösung von etwa 6 Hz ergibt.
Die Transformationen werden am PC mit Hilfe einer FFT, der Fast Fourier Transformation, durchgeführt. Es ist ein spezieller Algorithmus, der eine diskrete Transformation erheblich beschleunigt16 17 18. Voraussetzung ist allerdings eine Werteanzahl, die einer Zweierpotenz entspricht.
Im vorliegenden Projekt werden bei der Messung nicht nur die ermittelte Impulsantwort des Lautsprechers sowie deren Frequenzgang dargestellt, es erfolgt ebenfalls eine Darstellung der Sprungantwort, da sie ebenfalls recht aussagekräftig ist.
Ermittelt wird sie über die Integration der gemessenen Impulsantwort über der Zeit, denn ein integrierter Diracimpuls führt zur Sprungfunktion, was Abb. 3.13 noch einmal verdeutlicht.
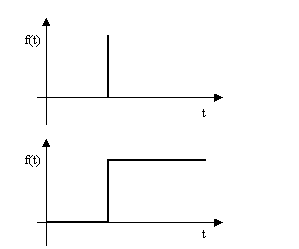
Abb. 3.13: Integration eines Diracimpulses
Selbst bei einer idealen Lautsprechermembran, einer Membran, die dem Sprung, also eine Bewegung vom Ruhepunkt in eine Auslenkposition, ohne jegliche Abweichungen vollzieht, sieht die Sprungantwort, gemessen über ein Mikrofon, also über das Medium Luft, wie folgt aus:
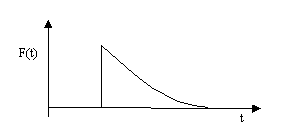
Abb. 3.14: Lautsprechersprungantwort
Nach der Auslenkung nähert sich der Schalldruck asymptotisch dem Normaldruck. Selbst ein idealer Lautsprecher besitzt somit Hochpaßverhalten, was auch klar ist, da ansonsten der statische Luftdruck für alle Zeiten erhöht sein würde.